Bilangan Prima adalah bilangan bulat positif yang hanya memiliki 2 faktor, yaitu 1 dan dirinya sendiri. Bilangan prima terkecil adalah 2. 1 bukan bilangan prima karena hanya memiliki 1 faktor yaitu 1. Faktor adalah bilangan bulat positif yang habis membagi suatu bilangan bulat. suatu bilangan bulat dikatakan habis dibagi oleh bilangan bulat jika hasil pembagiannya juga adalah bilangan bulat.
Lawan dari bilangan Prima adalah bilangan komposit. bilangan komposit adalah bilangan yang mempunyai lebih dari 2 faktor. semua bilangan bulat positif yang bukan bilangan prima selain 1adalah bilangan komposit. Kelipatan dari suatu bilangan prima adalah bilangan komposit.
Untuk mencari bilangan prima kita bisa menggunakan Saringan Eratosthenes. Saringan Eratosthenes adalah cara mencari bilangan prima yang dilakukan dengan menandai semua kelipatan bilangan bulat (khususnya bilangan prima) mulai dari bilangan prima terkecil yaitu 2. Algoritma Eratosthenes bisa diakhiri saat kita sudah menandai kelipatan dari akar kuadrat bilangan tertinggi yang diperiksa. Misalnya akar 100 akar kuadratnya adalah 10, sehingga kita cukup menandai kelipatan dari 2 hingga 10. Berikut ini, adalah langkah-langkah yang harus dilakukan untuk mencari bilangan prima dengan Algoritma Erathostenes:
- Buat tabel dengan kolom yang sama dengan barisnya.
- Tandai atau Coret angka 1 karena angka 1 hanya mempunyai satu faktor sehingga angka 1 sudah pasti bukan bilangan prima.
- Coret semua kelipatan "angka 2" selain dua.
- Setelah selesai mencoret kelipatan dua, coret kelipatan bilangan yang belum dicoret kecuali bilangan itu sendiri. Misalnya, jika kelipatan tiga dicoret maka angka 3 tidak perlu dicoret.
- Jika bilangan sudah dicoret, kelipatan bilangan tersebut tidak perlu dicari lagi. Karena otomatis semua kelipatan bilangan tersebut sudah dicoret sebelumnya, saat mencoret kelipatan dari faktornya. Misalnya kelipatan 4, 6, 8 dan 10 sudah dicoret ketika anda mencoret kelipatan 2.
- Jika sudah sampai ujung kolom anda bisa berhenti mencari kelipatan bilangan berikutnya. Karena jika jumlah kolom dan baris sama, sudah pasti kelipatan bilangan pada baris kedua dan seterusnya sudah dicoret.
- Angka yang dicoret selain satu adalah bilangan komposit.
- Angka yang belum dicoret adalah bilangan prima.
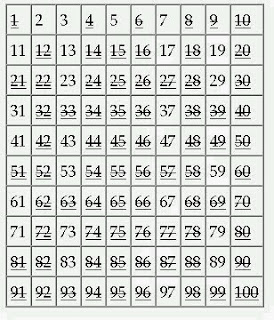
Untuk lebih jelasnya, berikut ini adalah contoh penerapan saringan Eratosthenes untuk mencari Bilangan prima di bawah 100.
- Buatlah tabel dengan jumlah kolom yang nilainya sama dengan atau lebih dari akar kuadrat dari bilangan maksimal yang akan dicari. Jika angka maksimalnya adalah bilangan kuadrat tabel yang dibuat jumlah kolomnya sama dengan barisnya. Misalnya, jika akan mencari bilangan prima kurang dari 100 maka jumlah kolomnya adalah 10 dan barisnya 10 yang merupakan akar kuadrat dari 100. Boleh saja membuat tabel dengan ukuran lainnya atau menuliskannya lurus kesamping, tetapi saya lebih suka dengan cara ini.
- Coret angka 1. karena 1 bukan bilangan prima.
- Coret semua kelipatan 2 selain 2. 2 adalah bilangan prima, dan kelipatannya adalah bilangan komposit karena jumlah faktornya lebih dari 2.
- Bilangan prima setelah 2 adalah 3, karena bilangan yg belum dicoret dan paling dekat selisihnya dengan "bilangan yang sudah dicari kelipatannya" adalah bilangan prima. Coret semua kelipatan 3 selain angka 3 itu sendiri.
- lewatkan 4 karena empat sudah dicoret.
- Bilangan prima berikutnya adalah 5. coret semua kelipatannya selain 5.
- lewati 6 karena sudah dicoret.
- Bilangan prima berikutnya yang belum ditandai adalah 7. tandai semua kelipatan 7 selain 7.
- Lewati 8, 9, dan 10 karena 8 dan 9 sudah dicoret yang menandakan bahwa bilangan tersebut adalah bilangan komposit.
- Bilangan prima di atas 10 (yang berada di ujung baris pertama dari tabel) tidak perlu dicari kelipatannya. Karena kelipatan bilangan prima setelah 10 yang kurang dari 100 adalah kelipatan semua bilangan yang kurang dari atau sama dengan 10 (akar kuadrat dari 100) yang sudah ditandai sebelumnya. Misalnya, kelipatan maksimal dari 11 adalah 99 yang merupakan hasil dari "11 dikalikan dengan 9". Jika n adalah bilangan yang dicari kelipatannya, saringan Eratosthenes bisa dihentikan jika n^2 (n pangkat 2) melebihi bilangan maksimal.
- Semua bilangan yang belum dicoret adalah bilangan prima. Pada tabel di atas kita bisa mengetahui jika bilangan yang merupakan bilangan prima di bawah 100 yaitu 2, 3, 5, 7, 11, 13, 17, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, dan 97.
6, 8, 9 dan 10 adalah bilangan komposit yang semua kelipatannya sudah ditandai sebelumnya saat kita menandai semua kelipatan bilangan prima. karena itu kita tidak perlu menandai kelipatan 6 karena kita sudah menandainya saat kita menandai kelipatan 2 dan 3. Saat mencoret kelipatan sebenarnya kita hanya perlu mencoret mulai dari nilai kuadrat bilangan tersebut. Misalnya 3 2 = 9, karena itu kita cukup mencoret dari angka 9.
Saya sudah menjelaskan penerapan Saringan Erathostenes untuk bilangan di bawah 100. Anda bisa juga menerapkan untuk bilangan diatas 100 walaupun mungkin akan merepotkan. Jika ingin menghemat kertas anda bisa cukup menuliskan bilangan ganjil saja di dalam tabel untuk mencari bilangan prima selain 2, sehingga jumlah kolom setengah dari jumlah barisnya. Karena satu-satunya bilangan genap yang merupakan bilangan prima adalah 2.